Research

My main reserach interests are in categorification in the context of low-dimensional topology, representation theory and mathematical physics. In particular, I am interested in topological quantum field theories (TQFTs) and link homology theories. I enjoy using tools from category theory as an organizing pricinple and doing explicit computations with graphical calculus to construct invariants in quantum topology.

If you’re interested in my work, feel free to contact me. I would be happy to chat or give a talk about my research!

My papers and preprints

2. A note on TQFTs for orientable 2-dimensional cobordisms

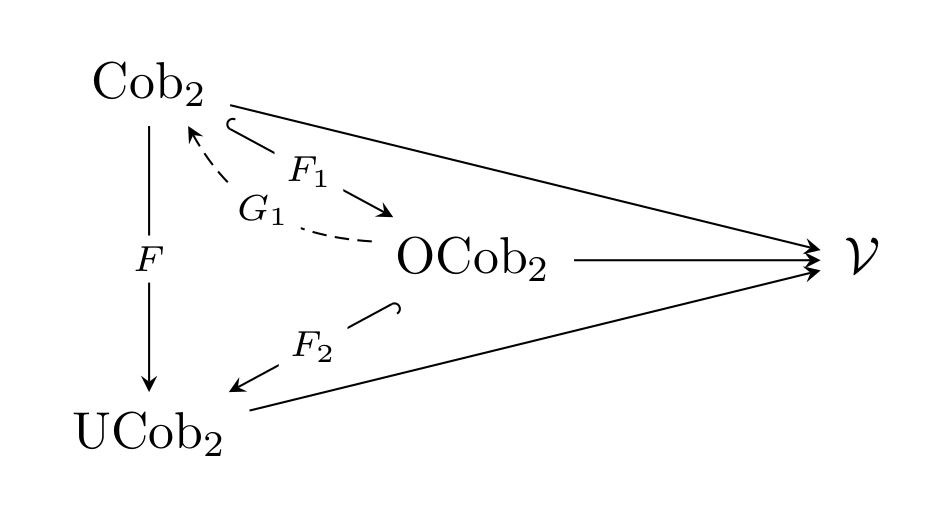Topological quantum field theories (TQFTs) are symmetric monoidal functors out of cobordism categories. In dimension two, oriented TQFTs are famously classified by commutative Frobenius algebras. In the unoriented setting, the classification requires additional data: an involution and a value assigned to the Möbius strip. In this work, we describe an intermediate framework that classifies 2-dimensional TQFTs for orientable cobordisms, in an appropriate sense. Our motivation arises from skein-theoretic models of surfaces embedded in 3-manifolds and Khovanov homology, where surfaces are often treated as unoriented, even though the associated 2-dimensional TQFTs themselves need not be fully unoriented.

joint with Paul Wedrich, arXiv:2511.19373, preprint, 2025

1. A construction of surface skein TQFTs and their extension to 4d 2-handlebodies

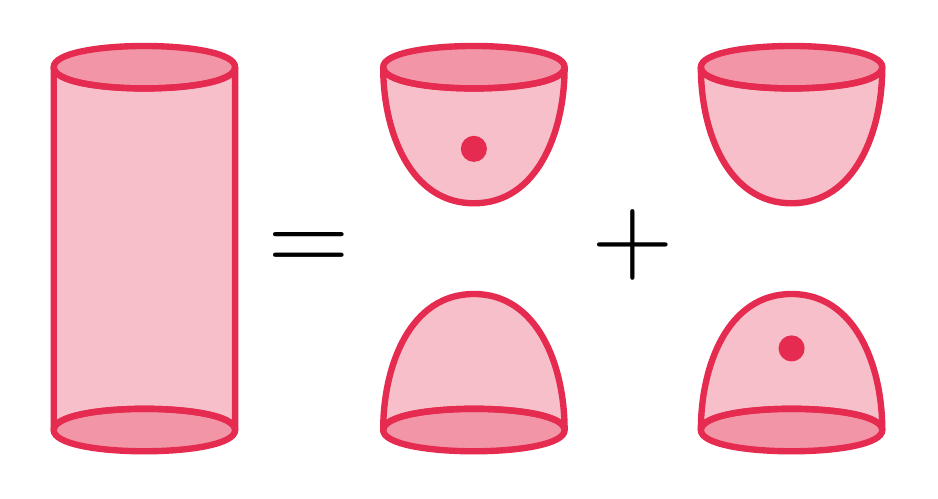For a commutative Frobenius algebra \(A\), we construct a \((2,3,3+\varepsilon)\)-dimensional TQFT \(\mathsf{AFK}_A\) that assigns to a 3-manifold a skein module of embedded \(A\)-decorated surfaces. These surface skein modules have been first defined by Asaeda–Frohman and Kaiser using skein relations that generalize the combinatorics of Bar-Natan’s dotted cobordisms. For 3-manifolds with boundary, we show that surface skein modules carry an action by a certain surface skein category associated with the boundary, which yields a gluing formalism. Our main result concerns a partial extension of \(\mathsf{AFK}_A\) to dimension 4, which uses an inductive state-sum construction following Walker. As an example, the equivariant version of Lee’s deformation of dotted cobordisms yields a TQFT that extends to 4-dimensional 2-handlebodies but not 3-handlebodies. Finally, we characterize the attachment of 4-dimensional 2-handles by means of a certain Kirby color and use it to compute the invariants of 4-dimensional 2-handlebodies in examples.

arXiv:2511.19352, preprint, 2025.

Other

• Elliptic genera in mathematics and physics and a generalization to G-manifolds, my M.Sc. thesis, available here, 2023.